When kids ask, “Why do I need to wear a mask?” it’s helpful to have a good understanding of exponential growth. Here are a few ideas for ways to unpack this powerful force.

Start by reading What does exponential growth mean in the context of covid-19?, a short article in the Washington Post. Then grab a chessboard (or draw the same number of squares on a large piece of paper).  Get some cheerios, jelly beans or something desirable and small.  

Look at the graph in the article.  Why does it look like a hockey stick?

To make it real, put one Cheerio on the chessboard and say: “Pretend these are jelly beans.  You win a bet and as your prize, I have to pay you one jelly bean on the first day. For the next 63 days, I give you double the jelly beans I gave you the day.  Sounds like a good deal?  There’s only one requirement:  you have to agree to eat the jelly beans you get each day.  Deal?”

Who wouldn’t accept that deal?  (Turns out, it’s not a good deal).

“On the first day, you get one jelly bean, the second day you get two and on the third day you get four. Then ask your kids to fill in the rest.  “On the fourth day I get eight jelly beans and on the fifth I get 16 and then I get 32!”

Things are looking good. The squares are too small and the Cheerios are too big so you’ll need to pull out a piece of paper and calculate that on the 10th day though, he or she will have 512 jelly beans to eat.  Are they phased yet?

Double that number on the 11th day. That would be 1,024 jelly beans.

By the 20th day, the number is over 500,000 jelly beans.  On the last day, the 64^th day, he would have 18,446,744,073,709,551,616 jelly beans. 

Draw a simple graph like this:

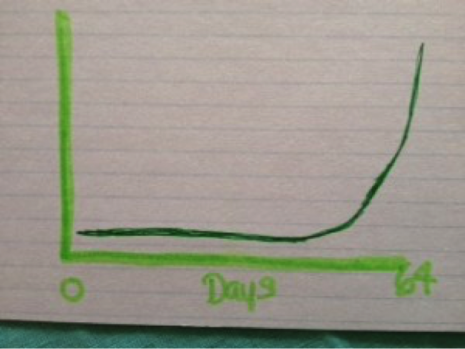
Talk about how sneaky doubling can be. And how once it gets going, it can be unstoppable.  Think of other examples together. If you are talking to teens, they may know examples of a small party that spiralled out of control (true story here) Another simple example is compound interest. Take two sticky notes. On one write “Money in the bank” on the other write: “Interest”. Say: If you leave your money in the bank (draw a link to interest), you received interest on that amount. The more money in your bank account, the more interest you accrue, (draw a link from interest to money in the bank) the more money in your bank account. 

If you leave your money in the bank, you are leveraging a simple closed loop of cause-and-effect known as compound interest, one Albert Einstein once may have called, “the most powerful force in the universe.”  

Now, go back to the question: Why do I need to wear a mask? Staying home. Not visiting friends.  Your behaviour multiplied by a lot of kids doing the right thing, can help “flatten” an exponential growth curve. Perhaps this is the simple lesson:  Our individual actions can combine to have positive or devastating impact on the whole.

Here are some other great resources for talking with kids about exponential growth:

Stories: 

Stories are a great way to learn about anything, even exponential growth. Here’s a system-based review I wrote about  One Grain of Rice by Demi (good for young and old) for the Waters Foundation.

For a similar story, try “Sissa and the Troublesome Trifles.  See I. G. Edmonds, Trickster Tales (Philadelphia: J. P. Lippincott Co.,1966) pp. 5-13.

Games: 

For a classic, hands-on example of underestimating the power of exponential growth see the Paper Fold game in the Systems Thinking Playbook and John Sterman’s original version below.

The Infection Game

See The Shape of Change and the Shape of Change Stocks and Flows, by Rob Quaden, Alan Ticotsky and Debra Lyneis, illustrated by Nathan Walker.  This paper-and-pencil game simulates the spread of an epidemic.  Best when played by a larger number of students – 35 is ideal.  

Movies/YouTube:  

This youtube clip by Dr. Albert Bartlett of U Colorado is worth every minute, more for teens and adults.

There are also some wonderfully clear examples of exponential growth on the Khan Academy site that explore compound interest and bacteria.

Websites/Blogs: Search “exponential growth” on the Water’s Center for Systems Thinking and Creative Learning Exchange websites.  Lots of great curriculum ideas.

Really good explanations, visuals and video clips on these two blogs:

Zimblog:  Understanding Exponential Growth

Growth Busters:  check out the documentary film and the blog

Try this: Find a young person between the ages of four and twenty-four. Show them a picture of a cow and ask, “If you cut a cow in half, do you get two cows?” Even the four-year-old will shout, “No way!” Children understand that a cow has certain parts—hearts, lungs, legs, brain, and more—that belong together and have to be arranged in a certain way for the cow to live. You cannot have the tail in the front and the nose in the back.

As adults, it is easy to miss this simple truth: a cow is a complex, living system, in the same way that the human body, a family, a classroom, a community, an organization, or an ocean is. A system is composed of parts and processes that interact over time—often in closed-loop patterns of cause and effect—to serve some purpose or function. Living systems, unlike a collection or “heap of stuff ,” share similar characteristics. In systems, it matters how the parts are arranged. at is why a cow cannot have the tail in the front and the nose in the back. And why a stomach does not work on its own, and the body does not work without a stomach. And systems often are connected to or nested within other systems (for instance, a person may be nested within a family, school, ecosystem, community, and nation).

Make the Shift: Systems Are the Context

Sounds simple, right? But here is the challenge: much of today’s education remains focused on discrete disciplines—for example, math, science, and English. Science is taught in one class. The bell rings. The student moves onto math and then, perhaps, to English—and never the twain shall meet. Such a fragmented approach reinforces the notion that knowledge is made up of many unrelated parts, leaving students well-trained to cope with obstacle-type or technical-based problems but less prepared to explore and understand complex systems issues. In medicine, for example, obstacle-type problems are those that can be clearly targeted and fixed, such as a broken arm or an acute disease, like appendicitis. A systems approach is more effective for chronic and complex diseases, such as diabetes, where the interaction of factors—lifestyle, family history, environment, etc.—also plays a role.

Issues such as climate change, economic breakdowns, food insecurity, biodiversity loss, and escalating conflict are matters not only of science, but also of geography, economics, philosophy, and history. They cut across several disciplines and are best understood when these domains are addressed together. Students and adults must be able to see such important issues as systems— elements interacting and affecting one another. In the case of climate change, a systems view shows the link between politics, policy (for example, legislation related to carbon emissions and deforestation), the natural sciences (particularly forests, which help stabilize the climate by absorbing heat-trap- ping emissions from factories and vehicles), and a person’s own consumption habits. Without a systems view, the complexity can be daunting, and the result is often policy resistance or, worse yet, polarization and political paralysis.

The excerpt above is from an article I recently wrote for World Watch Institute’s 2017 State of the World Report. For the complete article, click here.

Thank you to Draper L. Kauffman Jr., author of Systems I: An Introduction to Systems Thinking, for your inspired cow question, posed now over 30 years ago.

Illustration: Guy Billout, Art Direction, Milton Glaser. From “Connected Wisdom: Living Stories about Living Systems” by L. Booth Sweeney